Searching Algorithm

Linear Search (순차 탐색)

Linear search is a sequential searching algorithm where we start from one end and check every element of the list until the desired element is found. It is the simplest search algorithm.

  • 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 확인하는 방법
  • 보통 정렬되지 않은 리스트에서 데이터를 찾아야 할 때 사용한다.
  • 리스트 내에 데이터가 아무리 많아도 시간만 충분하다면 항상 원하는 원소(데이터)를 찾을 수 있다는 장점이 있다.

The following steps are followed to search for an element k = 1 in the list below.

Initial arrayArray to be searched for

  1. Start from the first element, compare k with each element x (Compare with each element).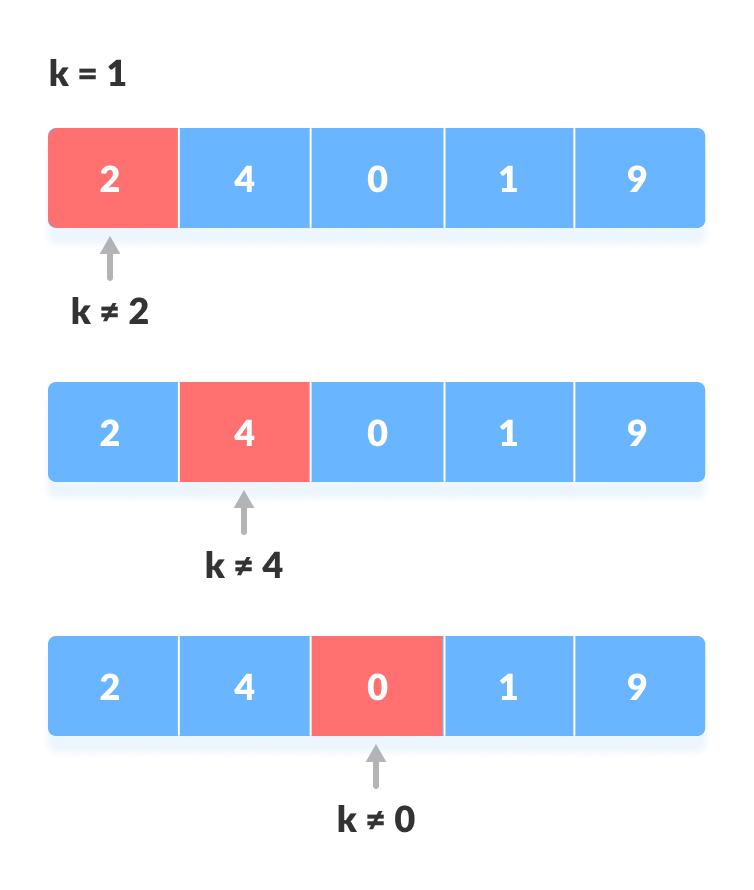

    Element not found

  2. If x == k, return the index.

    Element found

  3. Else, return not found.

Source Code

# 순차 탐색 소스코드 구현
def sequential_search(n, target, array):
	# 각 원소를 하나씩 확인하며
    for i in range(n):
    	# 현재 원소가 찾고자 하는 원소와 동일한 경우
        if array[i] == target:
        	return i+1  # 현재의 위치 반환(인덱스는 0부터 시작하므로 1 더하기)

print("생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.")
input_data = input().split()
n = int(input_data[0])  # 원소의 개수
target = input_data[1]  # 찾고자 하는 문자열

print("앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.")
array = input().split()

# 순차 탐색 수행 결과 출력
print(sequential_search(n, target, array))

Complexity

Time Complexity: $O(N)$

데이터의 개수가 N개일 때 최대 N번의 비교 연산이 필요하므로 순차 탐색의 최악의 경우 시간 복잡도는 O(N)이다.

Space Complexity: $O(1)$

Applications

For searching operations in smaller arrays (<100 items).

Binary Search (이진 탐색)

Binary Search is a searching algorithm for finding an element’s position in a sorted array.

In this approach, the element is always searched in the middle of a portion of an array.

  • 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법

  • 이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.

Binary search can be implemented only on a sorted list of items. If the elements are not sorted already, we need to sort them first.

이미 정렬된 10개의 데이터 중에서 값이 4인 원소를 찾는 예시를 살펴봅시다. img

[Step 1] 시작점: 0, 끝점: 9, 중간점: 4 (소수점 이하 제거) img

  • 중간점에 위치하는 값인 ‘8’과 찾고자 하는 값인 ‘4’와 비교하여 어떤 값이 더 큰지 비교

  • 만약 찾고자 하는 값보다 중간점의 값이 더 크다면 중간점에서부터 오른쪽에 위치한 값들은 확인할 필요가 없다.

[Step 2] 시작점: 0, 끝점: 3, 중간점: 1 (소수점 이하 제거) img

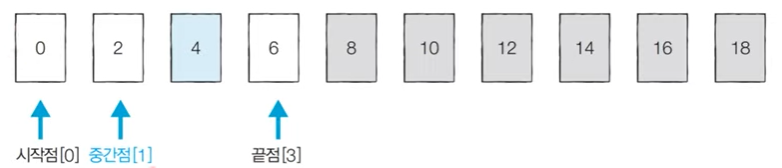
  • 중간점에 위치하는 값인 ‘2’보다 우리가 찾고자 하는 값인 ‘4’가 더 크기 때문에 중간점을 포함해서 왼쪽에 있는 데이터는 확인할 필요가 없다.

[Step 3] 시작점: 2, 끝점: 3, 중간점: 2 (소수점 이하 제거) img

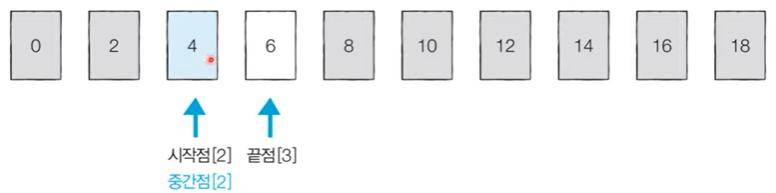
  • 우리가 찾고자 하는 값인 ‘4’는 인덱스 2에 위치한다는 것을 확인할 수 있다.

  • 전체 데이터의 개수는 10개이지만, 이진 탐색을 이용해 총 3번의 탐색으로 원소를 찾을 수 있다.

  • 절반씩 데이터를 줄어들도록 만든다는 점은 앞서 다룬 퀵 정렬과 공통점이 있다.

Complexity

Time Complexities

  • Best case complexity: O(1)
  • Average case complexity: O(log N)
  • Worst case complexity: O(log N)

Space Complexity

The space complexity of the binary search is O(1).

  • 단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 $log_2N$에 비례한다.
  • 다시 말해 이진 탐색은 탐색 범위를 절반씩 줄이며, 시간 복잡도는 $O(logN)$을 보장한다.

예를 들어 초기 데이터 개수가 32개일 때,

  1. 이상적으로 1단계를 거치면 16개가량의 데이터만 남는다.
  2. 2단계를 거치면 8개가량의 데이터만 남는다.
  3. 3단계를 거치면 4개가량의 데이터만 남는다.

Source code 1: Recursive Function

# 이진 탐색 소스코드 구현 (재귀 함수)
def binary_search(array, target, start, end):
	if start > end:
    	return None # 탐색하는 데이터가 존재하지 않는다고 생각
    mid = (start + end) // 2
    # 찾은 경우 중간점 인덱스 반환
    if array[mid] == target: 
    	return mid
    # 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
    elif array[mid] > target:
		return binary_search(array, target, start, mid-1)
    # 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
    else:
    	return binary_search(array, target, mid+1, end)
        
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))

# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n-1)
if result == None:
	print("원소가 존재하지 않습니다.")
else:
	print(result+1)

Source code 2

# 이진 탐색 소스코드 구현(반복문)
def binary_search(array, target, start, end):
	while start<=end:
    	mid = (start+end)//2
        # 찾은 경우 중간점 인덱스 반환
      if array[mid] == target:
      	return mid
      elif array[mid] > target:
      	end = mid-1
      else:
      	start = mid + 1
    return None
    
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))

# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1 )
if result == None:
	print("원소가 존재하지 않습니다.")
else:
	print(result+1)

Libraries

  • bisect_left(a, x): 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 왼쪽 인덱스를 반환
  • bisect_right(a, x): 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 오른쪽 인덱스를 반환

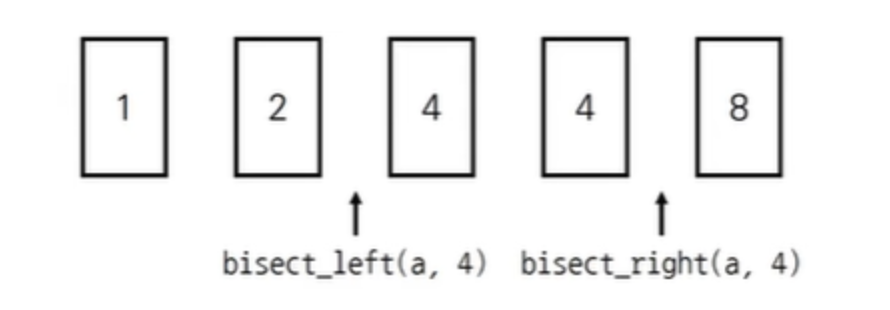
image-20230501145508313

from bisect import bisect_left, bisect_right

a = [1,2,4,4,8]
x = 4

print(bisect_left(a,x)) #2
print(bisect_right(a,x)) #4

Example 1: 값이 특정 범위에 속하는 데이터 개수 구하기

from bisect import bisect_left, bisect_right

# 값이 [left_value, right_value]인 데이터의 개수를 반환하는 함수
def count_by_range(a, left_value, right_value):
	  right_index = bisect_right(a, right_value)
    left_index = bisect_left(a, left_value)
    return right_index - left_index
    
# 배열 선언
a = [1,2,3,3,3,3,4,4,8,9]

# 값이 4인 데이터 개수 출력
print(count_by_range(a,4,4)) #2

# 값이 [-1,3] 범위에 있는 데이터 개수 출력
print(count_by_range(a,-1,3)) #6
  • 파라메트릭 서치란 최적화 문제를 결정 문제(‘예’ 혹은 ‘아니오’)로 바꾸어 해결하는 기법이다. 최적화 문제: 문제의 상황을 만족하는 특정 변수의 최소값, 최대값을 구하는 문제 (예시) 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제
  • 일반적으로 코딩 테스트에서 파라메트릭 서치 문제는 이진 탐색을 이용하여 해결할 수 있다.

Example 3: 떡볶이 떡 만들기

  • 오늘 동빈이는 여행 가신 부모님을 대신해서 떡집 일을 하기로 했습니다. 오늘은 떡볶이 떡을 만드는 날입니다. 동빈이네 떡볶이 떡은 재밌게도 떡볶이 떡의 길이가 일정하지 않습니다. 대신에 한 봉지 안에 들어가는 떡의 총 길이는 절단기로 잘라서 맞춰줍니다.
  • 절단기에 높이(H)를 지정하면 줄지어진 떡을 한 번에 절단합니다. 높이가 H보다 긴 떡은 H 위의 부분이 잘릴 것이고, 낮은 떡은 잘리지 않습니다.
  • 예를 들어 높이가 19, 14, 10, 17cm인 떡이 나란히 있고 절단기 높이를 15cm로 지정하면 자른 뒤 떡의 높이는 15, 14, 10, 15cm가 될 것입니다. 잘린 떡의 길이는 차례대로 4, 0, 0, 2cm입니다. 손님은 6cm만큼의 길이를 가져갑니다.
  • 손님이 왔을 때 요청한 총 길이가 M일 때 적어도 M만큼의 떡을 얻기 위해 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하세요.

img

  • 전형적인 이진 탐색 문제이자, 파라메트릭 서치 유형의 문제이다.
  • 코딩 테스트나 프로그래밍 대회에서는 보통 파라메트릭 서치 유형은 이진 탐색을 이용하여 해결한다.

img

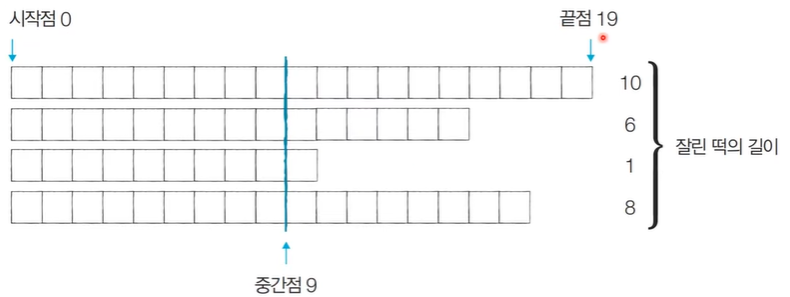
[Step 1] 시작점: 0, 끝점: 19, 중간점: 9 이때 필요한 떡의 크기: M=6이므로, 결과 저장 → 0과 19 사이의 중간점 9를 절단기 높이 H로 설정하면 얻을 수 있는 떡의 합은 (10+6+1+8)=25이다. 필요한 떡의 길이가 6보다 크기 때문에 시작점을 증가시킨다. img

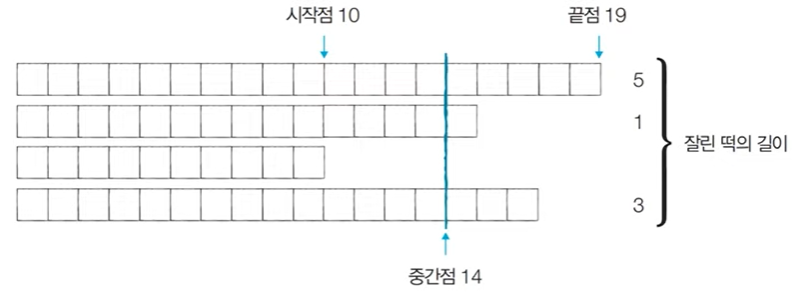
[Step 2] 시작점: 10, 끝점: 19, 중간점: 14 이때 필요한 떡의 크기: M=6이므로, 결과 저장 → 절단기 높이를 14로 설정하면 얻을 수 있는 떡의 합이 (5+1+3)=9이다. 여전히 필요한 떡의 길이인 6보다 크기 때문에 시작점을 증가시킨다. img

[Step 3] 시작점: 15, 끝점: 19, 중간점: 17 이때 필요한 떡의 크기: M=6이므로, 결과 저장하지 않음 → 필요한 떡의 길이인 6보다 작기 때문에 끝점을 감소시킨다. img

[Step 4] 시작점: 15, 끝점: 16, 중간점: 15 이때 필요한 떡의 크기: M=6이므로, 결과 저장 img

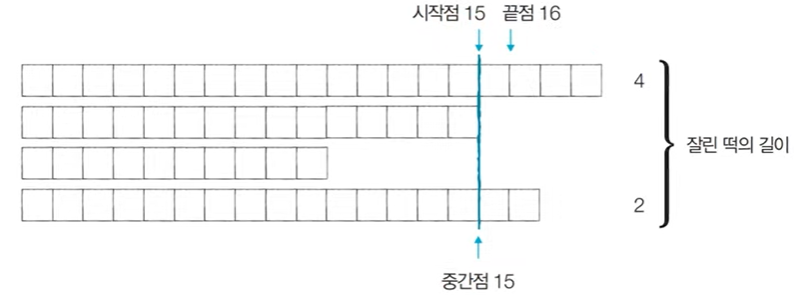
  • 이러한 이진 탐색 과정을 반복하면 답을 도출할 수 있다.
  • 중간점의 값은 시간이 지날수록 ‘최적화된 값’이 되기 때문에, 과정을 반복하면서 얻을 수 있는 떡의 길이 합이 필요한 떡의 길이보다 크거나 같을 때마다 중간점의 값을 기록하면 된다.
# 떡의 개수(N)와 요청한 떡의 길이(M)을 입력
n, m = list(map(int, input().split(' ')))
# 각 떡의 개별 높이 정보를 입력
array = list(map(int, input().split()))

# 이진 탐색을 위한 시작점과 끝점 설정
start = 0
end = max(array) #가장 긴 떡의 길이

# 이진 탐색 수행(반복적)
result = 0
while(start <= end):
		total = 0
    mid = (start + end) // 2
    for x in array:
    	# 잘랐을 때의 떡의 양 계산
        if x > mid:
        		total += x - mid
        # 떡의 양이 부족한 경우 더 많이 자르기(왼쪽 부분 탐색)
    if total < m:
    		end = mid - 1
        # 떡의 양이 충분한 경우 덜 자르기(오른쪽 부분 탐색)
    else:
    		result = mid  # 최대한 덜 잘랐을 때가 정답이므로, 여기에서 result에 기록
    		start = mid + 1
            
# 정답 출력
print(result)

Example 4: 정렬된 배열에서 특정 수의 개수 구하기

  • N개의 원소를 포함하고 있는 수열이 오름차순으로 정렬되어 있습니다. 이때 이 수열에서 x가 등장하는 횟수를 계산하세요. 예를 들어 수열 {1, 1, 2, 2, 2, 2, 3}이 있을 때 x=2라면, 현재 수열에서 값이 2인 원소가 4개이므로 4를 출력한다.
  • 단, 이 문제는 시간 복잡도 $O(log N)$으로 알고리즘을 설계하지 않으면 시간 초과 판정을 받습니다.

img

img

from bisect import bisect_left, bisect_right

# 값이 [left_value, right_value]인 데이터의 개수를 반환하는 함수
def count_by_range(array, left_value, right_value):
		right_index = bisect_right(array, right_value)
    left_index = bisect_left(array, left_value)
    return right_index - left_index
    
n, x = map(int, input().split())  # 데이터의 개수 N, 찾고자 하는 값 x 입력받기
array = list(map(int, input().split()))  # 전체 데이터 입력받기

# 값이 [x, x] 범위에 있는 데이터의 개수 계산
count = count_by_range(array, x, x)

# 값이 x인 원소가 존재하지 않는다면
if count == 0:
  print(-1)
# 값이 x인 원소가 존재한다면
else:
	print(count)

Leave a comment

You may also enjoy

Handling Missing Values

A perfect data set is usually a big win for any data scientist or machine learning engineer. Unfortunately, more often than not, datasets will have missing d...