Greedy Algorithm
The algorithm never reverses the earlier decision, even if the choice is wrong. It works in a top-down approach.
This algorithm may not produce the best result for all the problems. It’s because it always goes for the best local choice to produce the best global result.
Advantages and Drawback
- Pros: The algorithm is easier to describe.
- Pros: This algorithm can perform better than other algorithms (but not in all cases).
- Cons: The greedy algorithm doesn’t always produce the optimal solution. This is the major disadvantage of the algorithm.
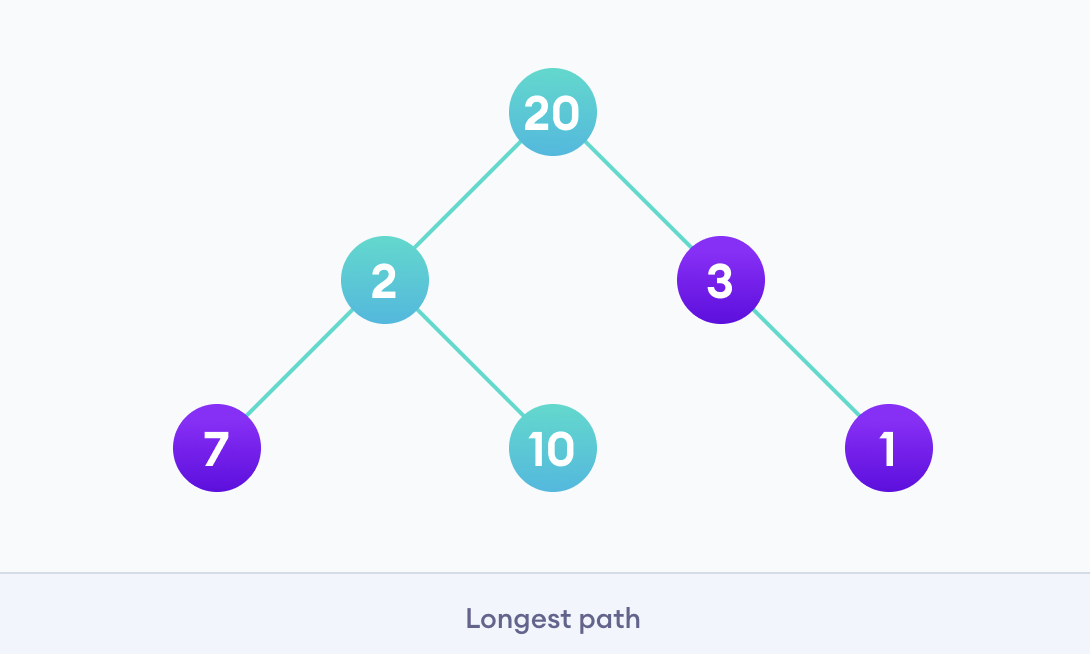
Let’s start with the root node 20. Our problem is to find the largest path. And the optimal solution at the moment is 3. Finally, the weight of an only child of 3 is 1. This gives us our final result 20 + 3 + 1 = 24.
Example1
당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한이 존재한다고 가정합니다. 손님에게 거슬러 주어야 할 돈이 N원일 때 거슬러 주어야 할 동전의 최소 개수를 구하세요. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수입니다.
[입력]: 1260 / [출력]: 6
n = 1260
count = 0
array = [500, 100, 50, 10] #큰 단위의 화폐부터
coin = 500
for coin in array:
count += n // coin #해당 화폐로 거슬러 줄 수 있는 동전의 개수 세기
n %= coin
print(count)
#500 * 2 + 100 * 2 + 50 * 1 + 10 * 1
- 화페의 종류 K개, Time complexity = O(K), 금액과는 무관하며, 동전의 총 종류에만 영향을 받음.
Example2: 1이 될 때까지
어떠한 수 N이 1이 될때까지 다음 두 과정 중 하나를 반복적으로 선택하여 수행하려고 합니다. 단, 두 번째 연산은 N이 아닌 K로 나누어 떨어질 때만 선택할 수 있습니다.
-
N에서 1을 뺍니다.
-
N을 K로 나눕니다.
예를 들어 N이 17, K가 4라고 가정합니다.
이때 1번의 과정을 한 번 수행하면 N은 16이 됩니다.
이후에 2번의 과정을 두번 수행하면 N은 1이 됩니다. 결과적으로 이 경우 전체 과정을 실행한 횟수는 3이 됩니다.
이는 N을 1로 만드는 최소 횟수입니다. N과 K가 주어질 때 N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 최소 횟수를 구하는 프로그램을 작성하세요
[입력]
25 5
[출력]
2
- 가능하면 최대한 많이 나누는 작업이 최적의 해를 보장할 수 있다.
# log시간 복잡도로 빠르게 작동 가능
n, k = map(int, input().split())
result = 0
while True:
# n이 k로 나누어 떨어지는 수가 될 때까지 빼기
target = (n // k) * k # 나누어떨어지는 가장 가까운 수를 구한다
result += (n - target) # 1씩 뺀 총 횟수가 더해짐
n = target # target이 나누어 떨어지는 수이므로 n에 할당
if n < k:
break
# k로 나누기
n //= k
result += 1
# n이 1보다 크다면 마지막으로 남은 수에 대하여 1씩 빼기
result += (n - 1)
print(result)
Example3: 곱하기 혹은 더하기
각 자리가 숫자(0부터 9)로만 이루어진 문자열 S가 주어졌을 때, 왼쪽부터 오른쪽으로 하나씩 모든 숫자를 확인하며 숫자 사이에 ‘*’ 혹은 ‘+’ 연산자를 넣어 결과적으로 만들어질 수 있는 가장 큰 수를 구하는 프로그램을 작성하세요.
단, +보다 *를 먼저 계산하는 일반적인 방식과는 달리, 모든 연산은 왼쪽에서부터 순서대로 이루어진다고 가정합니다.
예를 들어 02984라는 문자열이 주어지면, 만들어질 수 있는 가장 큰 수는 ((((0+2)9)8)*4) = 576 입니다.
[입력]
02984
[출력]
576
- 대부분의 경우 +보다 *가 더 값을 크게 만든다.
- 두 수 중에서 하나라도 ‘0’ 혹은 ‘1’인 경우 곱하기보다는 더하기를 수행하는 것이 효율적이다.
data = input()
result = int(data[0])
for i in range(1, len(data)):
num = int(data[i])
if num <= 1 or result <= 1:
result += num
else:
result *= num
print(result)
Example4: 모험가 길드
한 마을에 모험가가 N명 있습니다. 모험가 길드에서는 N명의 모험가를 대상으로 ‘공포도’를 측정했는데,’공포도’가 높은 모험가는 쉽게 공포를 느껴 위험 상황에서 제대로 대처할 능력이 떨어집니다.
모험가 길드장인 동빈이는 모험가 그룹을 안전하게 구성하고자 공포도가 X인 모험가는 반드시 X명 이상으로구성한 모험가 그룹에 참여해야 여행을 떠날 수 있도록 규정했습니다.
동빈이는 최대 몇 개의 모험가 그룹을 만들 수 있는지 궁금합니다. N명의 모험가에 대한 정보가 주어졌을 때, 여행을 떠날 수 있는 그룹 수의 최댓값을 구하는 프로그램을 작성하세요.
예를 들어, N = 5이고, 각 모험가의 공포도가 다음과 같다고 가정합시다.
2 3 1 2 2
이 경우 그룹 1에 공포도가 1, 2, 3인 모험가를 한 명씩 넣고, 그룹 2에 공포도가 2인 남은 두 명을 넣게 되면 총 2개의 그룹을 만들 수 있습니다. 또한 몇 명의 모험가는 마을에 그대로 남아 있어도 되기 때문에, 모든 모험가를 특정한 그룹에 넣을 필요는 없습니다.
[입력]
5
2 3 1 2 2
[출력]
2
n = int(input())
data = list(map(int, input().split()))
data.sort() #오름차순 정렬
result = 0 # 총 그룹의 수
count = 0 # 현재 그룹에 포함된 모험가의 수
for i in data: # 공포도를 낮은 것부터 하나씩 확인
count += 1 # 현재 그룹에 해당 모험가를 포함시키기
if count >= i: # 현재 그룹에 포함된 모험가의 수가 현재의 공포도 이상이라면, 그룹 결성
result += 1 # 총 그룹의 수 증가시키기
count = 0 # 현재 그룹에 포함된 모험가의 수 초기화
print(result) # 총 그룹의 수 출력
Leave a comment