Graph-based DSA

• 탐색(Search)이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정

• 대표적인 그래프 탐색 알고리즘으로 DFS와 BFS가 있습니다.

Recursive Function

자기 자신을 다시 호출하는 함수.

• 단순한 형태의 재귀 함수 예제
  • ‘재귀 함수를 호출합니다’라는 문자열을 무한히 출력
  • 어느 정도 출력하다가 최대 재귀 깊이 초과 메세지가 출력 됨

def recursive_function():
  print('재귀 함수를 호출합니다.')
  recursive_function()
  
recursive_function() 
#RecursionError: maximum recursion depth exceeded while calling a Python object

• 재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수의 종료 조건을 반드시 명시.
• 종료 조건을 제대로 명시하지 않으면 함수가 무한히 호출될 수 있음.
• 스택 자료구조를 이용.

def recursive_function(i):
    if i == 100:
        return
    print(i, '번째 재귀함수에서', i +1, '번째 재귀함수를 호출합니다.')
    recursive_function(i+1)
    print(i, '번째 재귀함수를 종료합니다.')
recursive_function(1)

Factorial value (팩토리얼 값 구하기)

5! = 5 * 4 * 3 * 2 * 1

# 5-5 DFS,BFS 팩토리얼
#재귀 미사용
def normal(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result

# 재귀 사용
def facto(n):
    if n == 1:
        return 1
    return n * facto(n-1)
  
print(normal(5)) #120
print(facto(5)) #120

Complexity

O(N). n의 길이만큼 순회하며 진행합니다.

Euclidean algorithm( 유클리드 호제법)

두 개의 자연수에 대한 최대공약수

• 두 자연수 A,B에 대하여 (A, > B) A를 B로 나눈 나머지를 R이라고 합니다.
  • R = A % B
• 이 때 A와 B의 최대 공약수를 B와 R의 최대 공약수와 같습니다.
  • GCD(A,B) = GCD(B,R)

유클리드 호제법에 대한 증명보다는 예시를 통해 설명하겠습니다. a>b라는 조건에 대해서 GCD(b, a%b)를 호출합니다. 이 때 항상 b > a%b이기 때문에 다음 호출에서 a > b의 조건도 만족하게 됩니다.

단계	A	B
1	192	162
2	162	30
3	30	12
4	12	6

풀이과정

def GCD(a, b):
    if a % b == 0:
        return b
    return GCD(b, a % b)


print(GCD(192, 162)) # 6

Depth First Search (DFS)

Depth-first Search or Depth-first traversal is a recursive algorithm for searching all the vertices of a graph or tree data structure.

• DFS에서 스택을 사용할 때 구현상 스텍 라이브러리 대신에 재귀 함수를 이용함.
• 깊이 우선 탐색, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘.
• 스택 자료구조 혹은 재귀 함수를 이용.

A standard DFS implementation puts each vertex of the graph into one of two categories:

1. Visited
2. Not Visited

The purpose of the algorithm is to mark each vertex as visited while avoiding cycles.

The DFS algorithm works as follows:

1. Start by putting any of the graph’s vertices on top of a stack.
2. Take the top item of the stack and add it to the visited list.
3. Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the top of the stack.

4. Keep repeating steps 2 and 3 until the stack is empty.

5. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 합니다.
6. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 있다면 그 노드를 스택에 넣고 방문처리합니다.
   • 방문하지 않은 인접한 노드가 없으면 최상단 노드를 꺼냅니다.
7. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복합니다.

Example 1

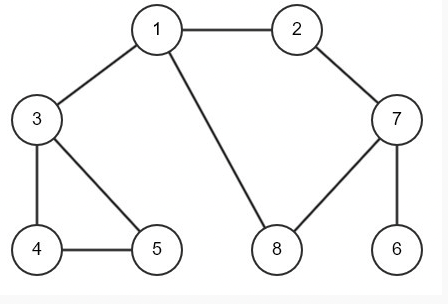
[Step 1] 시작 노드인 ‘1’을 스택에 삽입하고 방문처리를 한다.

[Step 2] 스택의 최상단 노드인 '1'에 방문하지 않은 인접 노드 '2','3','8'이 있다. 이 중에서 가장 작은 노드인 ‘2’를 스택에 넣고 방문 처리를 한다.

[Step 3] 스택의 최상단 노드인 '2'에 방문하지 않은 인접 노드 '7'이 있다. 따라서 ‘7’번 노드를 스택에 넣고 방문 처리를 한다.

[Step 4] 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '6','8'이 있다. 이 중에서 가장 작은 노드인 ‘6’을 스택에 넣고 방문 처리를 한다.

[Step 5] 스택의 최상단 노드인 '6'에 방문하지 않은 인접 노드가 없다. 따라서 스택에서 ‘6’번 노드를 꺼낸다.

[Step 6] 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '8'이 있다. 따라서 ‘8’번 노드를 스택에 넣고 방문 처리를 한다.

이러한 과정을 반복하였을 때 전체 노드의 탐색 순서(스택에 들어간 순서)는 다음과 같다. 탐색 순서: 1 → 2 → 7 → 6 → 8 → 3 → 4 → 5

1 2 7 6 8 3 4 5 

# 방문 기준: 번호가 낮은 인접 노드부터
# 노드 0번은 없음, 2차원 리스트
graph = [
    [], #index = 0
    [2, 3, 8],#해당 노드에 인접한 노드가 무엇인지 담아둠.
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

'''
graph : 그래프
v : 시작 노드
visited[i] : i 번째 노드 방문 여부
'''


def dfs(graph, v, visited):
    visited[v] = True
    print(v, end=' ')

    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)

# 각 노드가 방문된 정보를 표현 (1차원 리스트)
visited = [False] * 9 #아직 하나도 방문하지 않은 것으로 처리 (8+1)
dfs(graph, 1, visited)

Example 2: Connected components, 음료수 얼려먹기

NXM 크기의 얼음 틀이 있습니다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시됩니다. 구멍이 뚫려 있는 부분끼리 상,하,좌,우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주한다. 이때 얼음 틀의 모양이 주어졌을 때 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하세요. 다음의 4X5 얼음 틀 예시에서는 아이스크림이 총 3개 생성됩니다.

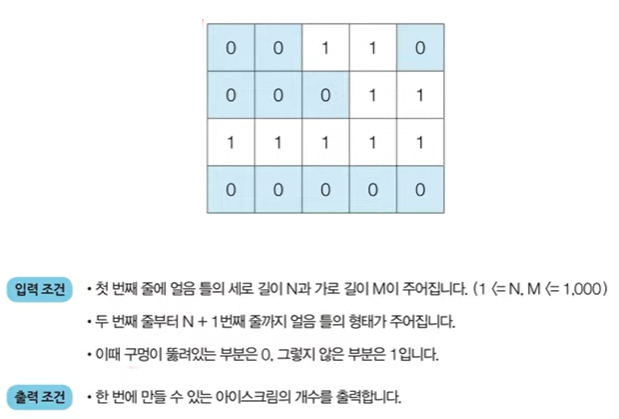
• 이 문제는 DFS 혹은 BFS로 해결할 수 있다.
• 얼음을 얼릴 수 있는 공간이 상,하,좌,우로 연결되어 있다고 표현할 수 있으므로 그래프 형태로 모델링 할 수 있다.

DFS를 활용하는 알고리즘은 다음과 같다. 1. 특정한 지점의 주변 상,하,좌,우를 살펴본 뒤에 주변 지점 중에서 값이 '0'이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다.

2. 방문한 지점에서 다시 상,하,좌,우를 살펴보면서 방문을 진행하는 과정을 반복하면, 연결된 모든 지점을 방문할 수 있다.

3. 모든 노드에 대하여 1~2번의 과정을 반복하며, 방문하지 않은 지점의 수를 카운트한다.

입력에 따라서 0의 연결 요소의 갯수를 구하여 출력하세요.

# DFS로 특정 노드를 방문하고 연결된 모든 노드들도 방문
def dfs(x,y):
	# 주어진 범위를 벗어나는 경우에는 즉시 종료
    if x<=-1 or x>=n or y<=-1 or y>=m:
    	return False
    # 현재 노드를 아직 방문하지 않았다면
    if graph[x][y] == 0:
    	# 해당 노드 방문 처리
        graph[x][y] = 1
        # 상,하,좌,우의 위치들도 모두 재귀적으로 호출
        dfs(x-1, y)
        dfs(x, y-1)
        dfs(x+1, y)
        dfs(x, y+1)
        return True
    return False

# N, M을 공백을 기준으로 구분하여 입력 받기
n, m = map(int, input().split())

# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
	graph.append(list(map(int, input())))

# 모든 노드(위치)에 대하여 음료수 채우기
result = 0
for i in range(n):
	for j in range(m):
    	# 현재 위치에서 DFS 수행
        if dfs(i,j) == True:
        	result += 1

print(result)  # 정답 출력

입력

4 5
00110
00011
11111
00000

출력

3

각 칸에 대해서 방문 여부를 저장합니다. 그리고 왼쪽위부터 오른쪽아래까지 방문하지 않았으면 DFS/BFS 중 하나를 수행합니다. DFS/BFS를 최초로 시작하는 횟수가 연결요소의 갯수입니다. 이미 방문한 노드는 건너뜁니다.

# dfs 풀이
n, m = map(int, input().split())

graph = []
for i in range(n):
    graph.append(list(map(int, input())))

visited = [[False] * m for i in range(n)]

dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]

def dfs(x, y):
    global graph, visited
    visited[x][y] = True

    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]

        # 범위를 벗어난 경우 제외
        if (nx < 0 or n <= nx) or (ny < 0 or m <= ny):
            continue
        # 벽을 만난 경우 제외
        if graph[nx][ny] == 1:
            continue
        if graph[nx][ny] == 0 and not visited[nx][ny]:
            dfs(nx, ny)


ans = 0
for x in range(n):
    for y in range(m):
        if graph[x][y] == 0 and not visited[x][y]:
            ans += 1
            # print('({}, {})'.format(x, y))
            dfs(x, y)

print(ans)

#
#4 5
#00110
#00011
#11111
#00000

Complexity

The time complexity of the DFS algorithm is represented in the form of O(V + E), where V is the number of nodes and E is the number of edges.

The space complexity of the algorithm is O(V).

Applications

1. To find the path
2. To test if the graph is bipartite
3. For finding the strongly connected components of a graph
4. For detecting cycles in a graph

Breadth-First Search (BFS)

• 너비 우선 탐색이라고도 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘.

• 큐자료를 이용

The algorithm works as follows:

1. Start by putting any one of the graph’s vertices at the back of a queue.

2. Take the front item of the queue and add it to the visited list.

3. Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the back of the queue.

4. Keep repeating steps 2 and 3 until the queue is empty.

5. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
6. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
7. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.

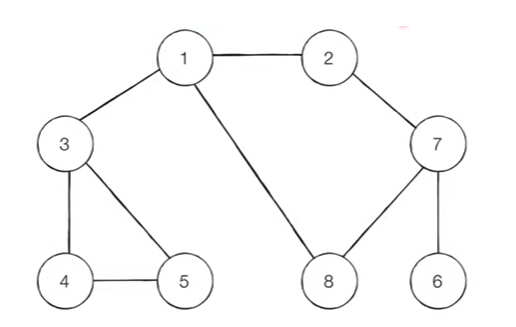
[Step 1] 시작 노드인 ‘1’을 큐에 삽입하고 방문 처리를 한다.

[Step 2] 큐에서 노드 ‘1’을 꺼내 방문하지 않은 인접노드 ‘2’,’3’,’8’을 큐에 삽입하고 방문 처리한다.

[Step 3] 큐에서 노드 ‘2’를 꺼내 방문하지 않은 인접 노드 ‘7’을 큐에 삽입하고 방문 처리한다.

[Step 4] 큐에서 노드 ‘3’을 꺼내 방문하지 않은 인접 노드 ‘4’,’5’를 큐에 삽입하고 방문 처리한다.

[Step 5] 큐에서 노드 ‘8’을 꺼내고 방문하지 않은 인접 노드가 없으므로 무시한다.

이러한 과정을 반복하여 전체 노드의 탐색 순서(큐에 들어간 순서)는 다음과 같다. 탐색 순서: 1 → 2 → 3 → 8 → 7 → 4 → 5 → 6

Example 1

from collections import deque

# BFS 메서드 정의
def bfs(graph, start, visited):
	# 큐(Queue) 구현을 위해 deque 라이브러리 사용
    queue = deque([start])
    # 현재 노드를 방문 처리
    visited[start] = True
    # 큐가 빌 때까지 반복
    while queue:
    	# 큐에서 하나의 원소를 뽑아 출력하기
        v = queue.popleft()
        print(v, end=' ')
        # 아직 방문하지 않은 인접한 원소들을 큐에 삽입
        for i in graph[v]:
        	if not visited[i]:
            	queue.append(i)
                visited[i] = True

# 각 노드가 연결된 정보를 표현(2차원 리스트)
graph = [
	[],
    [2,3,8],
    [1,7],
    [1,4,5],
    [3,5],
    [3,4],
	[7],
    [2,6,8],
    [1,7]
]

# 각 노드가 방문된 정보를 표현 (1차원 리스트)
visited = [False]*9

# 정의된 BFS 함수 호출
bfs(graph, 1, visited)

Example 2: 최단경로, 미로탈출

• 동빈이는 NXM 크기의 직사각형 형태의 미로에 갇혔습니다. 미로에는 여러 마리의 괴물이 있어 이를 피해 탈출해야 합니다.
• 동빈이의 위치는 (1,1)이며 미로의 출구는 (N,M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있습니다. 이때 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있습니다. 미로는 반드시 탈출할 수 있는 형태로 제시됩니다.
• 이때 동빈이가 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하세요. 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산합니다.

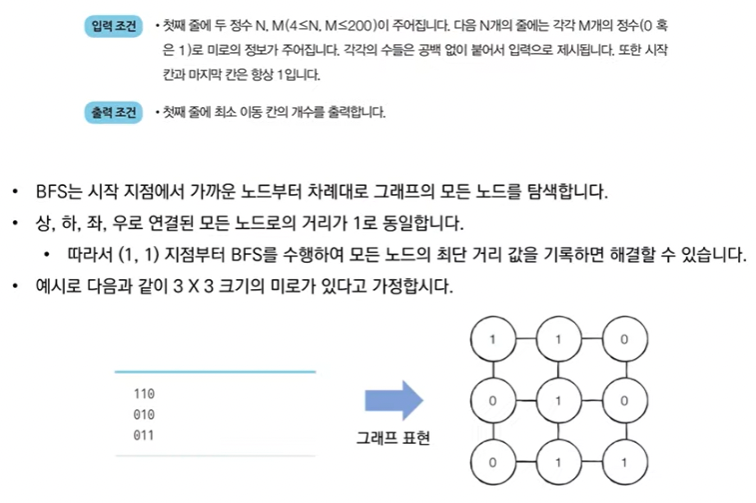
[Step 1] 처음에 (1,1)의 위치에서 시작한다.

[Step 2] (1,1) 좌표에서 상,하,좌,우로 탐색을 진행하면 바로 옆 노드인 (1,2) 위치의 노드를 방문하게 되고 새롭게 방문하는 (1,2) 노드의 값을 2로 바꾸게 된다.

[Step 3] 마찬가지로 BFS를 계속 수행하면 결과적으로 다음과 같이 최단 경로의 값들이 1씩 증가하는 형태로 변경된다.

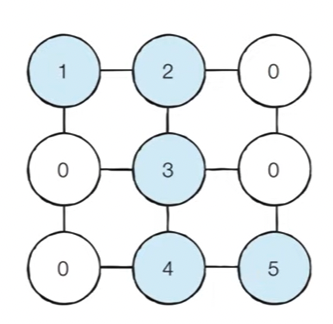
# BFS 소스코드 구현
def bfs(x,y):
	# 큐(Queue) 구현을 위해 deque 라이브러리 사용
    queue = deque()
    queue.append((x,y))
	
    # 큐가 빌 때까지 반복하기
    while queue:
    	x,y =queue.popleft()
        # 현재 위치에서 4가지 방향으로의 위치 확인
        for i in range(4):
        	nx = x+dx[i]
            ny = y+dy[i]
            # 미로 찾기 공간을 벗어난 경우 무시
            if nx<0 or nx>=n or ny<0 or ny>=m:
            	continue
            # 벽인 경우 무시
            if graph[nx][ny] == 0:
            	continue
            # 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
            if graph[nx][ny] == 1:
            	graph[nx][ny] = graph[x][y]+1
                queue.append((nx,ny))
                
    # 가장 오른쪽 아래까지의 최단 거리 반환
    return graph[n-1][m-1]
    
from collections import deque

# N,M을 공백을 기준으로 구분하여 입력 받기
n,m = map(int, input().split())

# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
	graph.append(list(map(int, input())))
    
# 이동할 네 가지 방향 정의(상,하,좌,우)
dx = [-1,1,0,0]
dy = [0,0,-1,1]

# BFS를 수행한 결과 출력
print(bfs(0,0))

Complexity

The time complexity of the BFS algorithm is represented in the form of O(V + E), where V is the number of nodes and E is the number of edges.

The space complexity of the algorithm is O(V).

Applications

1. To build index by search index
2. For GPS navigation
3. Path finding algorithms
4. In Ford-Fulkerson algorithm to find maximum flow in a network
5. Cycle detection in an undirected graph
6. In minimum spanning tree

DFS, BFS 문제 구분

• DFS: 경우의 수를 구하는 문제
• BFS: 최단거리 또는 최소횟수를 구하는 문제