Floyd-Warshall Algorithm

플로이드 워셜 알고리즘 개요

• 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다.
• 플로이드 워셜(Floyd-Warshall) 알고리즘은 다익스타라 알고리즘과 마찬가지로 단계별로 거쳐 가는 노드를 기준으로 알고리즘을 수행한다. - 다만 매 단계마다 방문하지 않은 노드 중에 최단 거리를 갖는 노드를 찾는 과정이 필요하지 않다.
• 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장한다.
• 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속한다.

플로이드 워셜 알고리즘

• 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인한다. a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사한다.
• 점화식은 다음과 같다.

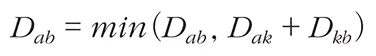
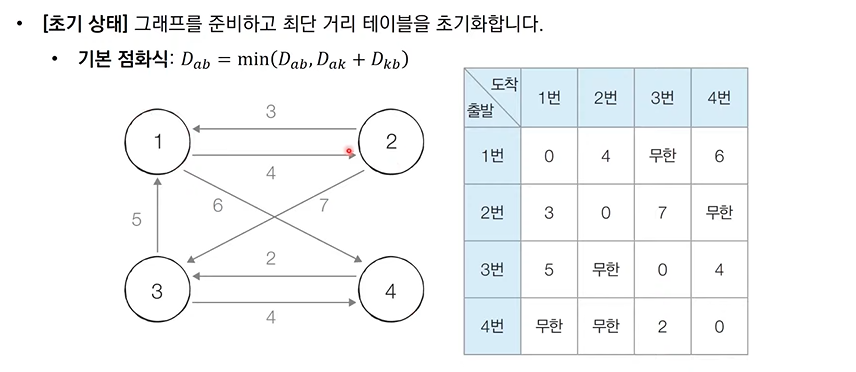
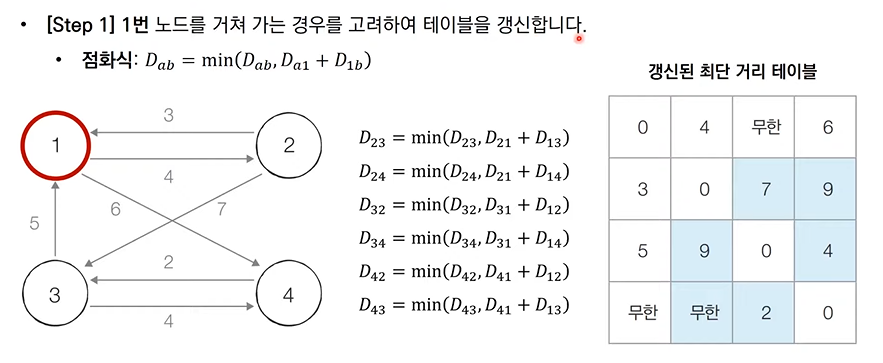
플로이드 워셜 알고리즘: 동작 과정 살펴보기

플로이드 워셜 알고리즘: 코드

INF = int(1e9)  # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 무한으로 초기화
graph = [[INF]*(n+1) for _ in range(n+1)]

# 자기 자신에게 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n+1):
	for b in range(1, n+1):
    	if a == b:
        	graph[a][b] = 0
            
# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
	# A에서 B로 가는 비용은 C라고 설정
    a, b, c = map(int, input().split())
    graph[a][b] = c
    
# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n+1):
	for a in range(1, n+1):
    	for b in range(1, n+1):
        	graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])
            
# 수행된 결과를 출력
for a in range(1, n+1):
	for b in range(1, n+1):
    	# 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
        if graph[a][b] == INF:
        	print("INFINITY", end=" ")
        # 도달할 수 있는 경우 거리를 출력
        else:
        	print(graph[a][b], end=" ")
    print()

플로이드 워셜 알고리즘 성능 분석

• 노드의 개수가 N개일 때 알고리즘상으로 N번의 단계를 수행한다.

• 각 단계마다 O(N2)의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려한다.

• 따라서 플로이드 워셜 알고리즘의 총 시간 복잡도는

  O(N3)

  이다.

  - 플로이드 워셜 알고리즘이 사용되어야 하는 문제에서는 노드의 개수가 500개 이하의 작은 값으로 구성된 경우가 많다. - 또한 단순히 계산하더라도 다시말해 노드의 개수가 500개가 된다고해도 500X500X500은 1억이 넘어가는 수이기 때문에 시간제한이 넉넉하지 않다면 시간 초과 판정을 받을 수 있다.

  "최단 거리를 구해야 하는 문제가 출제되었을 때 다익스트라, 플로이드 워셜 등 다양한 알고리즘들 중에서 어떤 알고리즘을 사용하는게 적절한지에 대해 고민해봐야 한다."

[문제2] 미래 도시: 문제 설명

• 미래 도시에는 1번부터 N번까지의 회사가 있는데 특정 회사끼리는 서로 도로를 통해 연결되어 있다. 방문 판매원 A는 현재 1번 회사에 위치해 있으며, X번 회사에 방문해 문건을 판매하고자 한다.
• 미래 도시에서 특정 회사에 도착하기 위한 방법은 회사끼리 연결되어 잇는 도로를 이용하는 방법이 유일하다. 또한 연결된 2개의 회사는 양방향으로 이동할 수 있다. 공중 미래 도시에서 특정 회사와 다른 회사가 도로로 연결되어 있다면, 정확히 1만큼의 시간으로 이동할 수 있다.
• 또한 오늘 방문 판매원 A는 기대하던 소개팅에도 참석하고자 한다. 소개팅의 상대는 K번 회사에 존재한다. 방문 판매원 A는 X번 회사에 가서 물건을 판매하기 전에 먼저 소개팅 상대의 회사에 찾아가서 함께 커피를 마실 예정이다. 따라서 방문 판매원 A는 1번 회사에서 출발하여 K번 회사를 방문한 뒤에 X번 회사로 가는 것이 목표다. 이때 방문 판매원 A는 가능한 한 빠르게 이동하고자 한다.
• 방문 판매원이 회사 사이를 이동하게 되는 최소 시간을 계산하는 프로그램을 작성하시오.

INF = int(1e9)  # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n, m = map(int, input().split())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF]*(n+1) for _ in range(n+1)]

# 자기 자신에게 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n+1):
	for b in range(1, n+1):
    	if a == b:
        	graph[a][b] = 0

# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
	# A와 B가 서로에게 가는 비용은 1이라고 설정
    a,b = map(int, input().split())
    graph[a][b] = 1
    graph[b][a] = 1
    
# 거쳐 갈 노드 X와 최종 목적지 노드 K를 입력받기
x, k = map(int, input().split())

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n+1):
	for a in range(1, n+1):
    	for b in range(1, n+1):
        	graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])

# 수행된 결과를 출력
distance = graph[1][k] + graph[k][x]

# 도달할 수 없는 경우, -1을 출력
if distance >= INF:
	print("-1")
# 도달할 수 있다면, 최단 거리를 출력
else:
	print(distance)