Dynamic Programming

Dynamic Programming is a technique in computer programming that helps to efficiently solve a class of problems that have overlapping subproblems and optimal substructure properties.

If any problem can be divided into subproblems, which in turn are divided into smaller subproblems, and if there are overlapping among these subproblems, then the solutions to these subproblems can be saved for future reference. In this way, the efficiency of the CPU can be enhanced. This method of solving a solution is referred to as dynamic programming.

Such problems involve repeatedly calculating the value of the same subproblems to find the optimum solution.

  • 다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법이다.

  • 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다.

  • 다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(Top-down과 Bottom-up)으로 구성된다.

  • 다이나믹 프로그래밍은 동적 계획법이라고도 부른다.

일반적인 프로그래밍 분야에서의 동적(Dynamic)이란 어떤 의미를 가질까?

  • 자료구조에서 동적 할당(Dynamic Allocation)은 ‘프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법’을 의미한다.
  • 반면에 다이나믹 프로그래밍에서 ‘다이나믹’은 별다른 의미 없이 사용된 단어이다.

Conditions on Dynamic Programming

  1. 최적 부분 구조(Optimal Substructure) 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
  2. 중복되는 부분 문제(Overlapping Subproblem) 동일한 작은 문제를 반복적으로 해결해야 한다.

Dynamic Programming Example

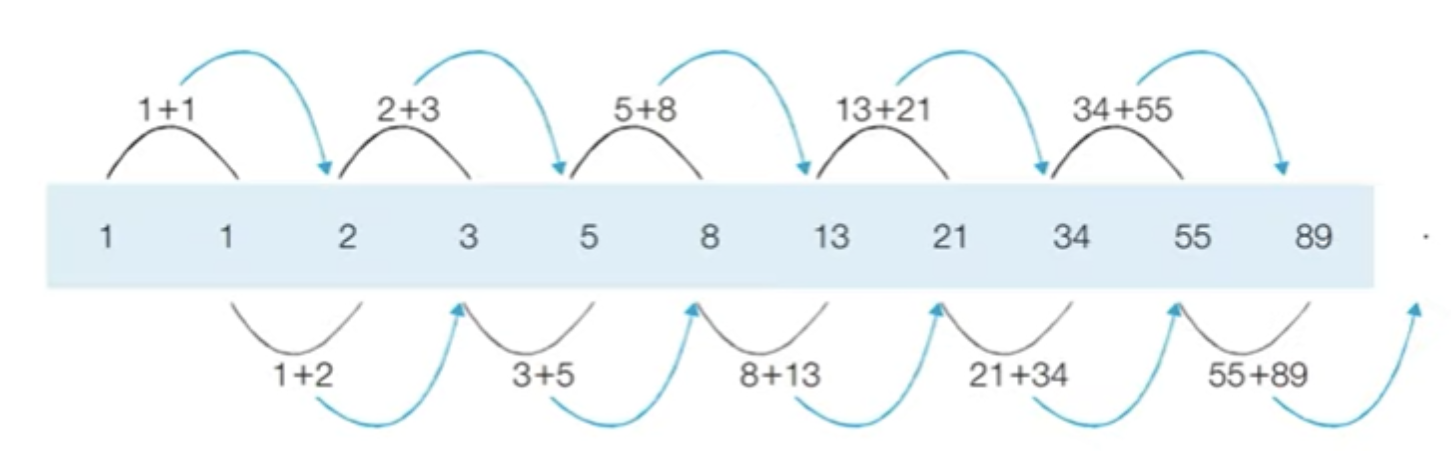
Let’s find the Fibonacci sequence up to the 5th term. A Fibonacci series is a sequence of numbers in which each number is the sum of the two preceding ones. img

image-20230502001124441

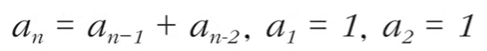
Source Code1: Recursion

# 피보나치 함수(Fibonacci Function)을 재귀함수로 구현
def fibo(x):
  if x==1 or x==2:
    	return 1
  return fibo(x - 1) + fibo(x - 2)
    
print(fibo(4)) #3

문제점: Time Complexity

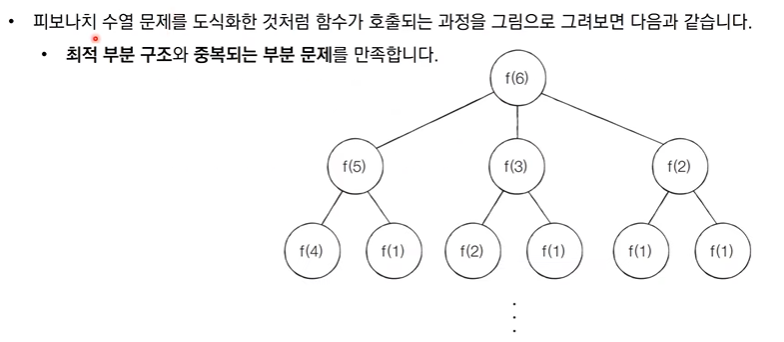
  • 단순 재귀 함수로 피보나치 수열을 해결하면 지수 시간 복잡도를 가지게 된다.
  • 다음과 같이 f(2)가 여러 번 호출 되는 것을 확인할 수 있다. (중복되는 부분 문제 발생: 계산한 것을 미리 저장해놓지 않으면 수행시간 측면에서 비효율적)

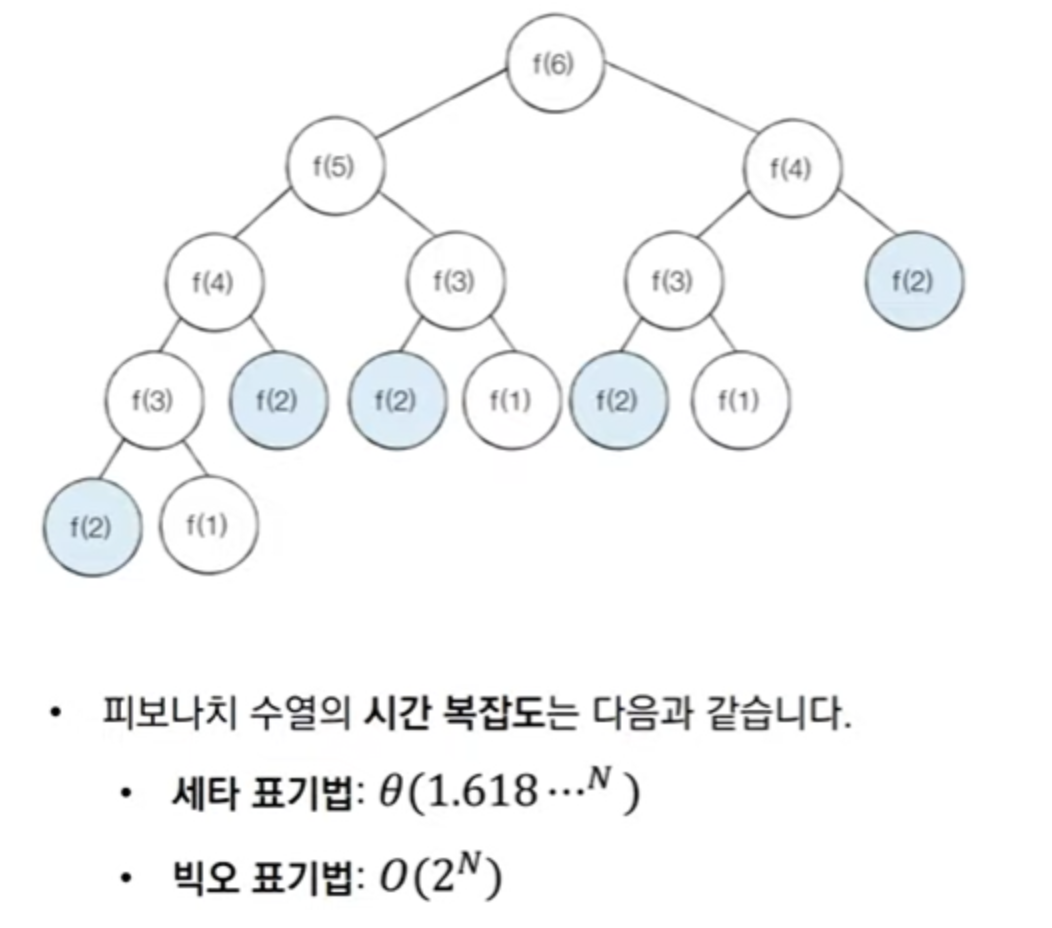
image-20230502001352035

  • 빅오 표기법을 기준을 f(30)을 계산하기 위해 약 10억가량의 연산을 수행해야 한다. - 즉, f(n)에서 n이 커지면 커질수록 반복해서 호출하는 수가 많아진다. - 이처럼 피보나치 수열의 점화식을 재귀 함수를 사용해 만들 수는 있지만, 단순히 매번 계산하도록 하면 문제를 효율적으로 해결할 수 없다.

Dynamic Programming

  • 다이나믹 프로그래밍의 사용 조건을 만족하는지 확인한다. 1. 최적 부분 구조: 큰 문제를 작은 문제로 나눌 수 있다. 2. 중복되는 부분 문제: 동일한 작은 문제를 반복적으로 해결한다.
  • 피보나치 수열은 다이나믹 프로그래밍의 사용 조건을 만족한다.

Top-down (Memoization)

  • 한 번 계산한 결과를 메모리 공간에 메모하는 기법 - 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져온다. - 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 함.
  • DP, D

Memoization 동작 분석 (피보나치 수열)

img

  • 재귀적으로 호출하게 되면 6번째 수를 구하기 위해 5번째 수를 호출하게 되고, 5번째 수를 구하기 위해 4번째 수, 4번째 수를 구하기 위해 3번째 수를 호출하게 된다.
  • 결과적으로 1번째 수와 2번째 수는 바로 ‘1’이란 값을 리턴하기 때문에 3번째 값이 구해지게 된다.
  • 메모이제이션을 이용하는 경우 피보나치 수열 함수의 시간 복잡도는 $O(N)$입니다.
d = [0]*100

def fibo(x):
	print('f('+str+')', end=' ')
    if x==1 or x==2:
    	return 1
    if d[x] != 0:
    	return d[x]
    d[x] = fibo(x-1) + fibo(x-2)
    return d[x]

fibo(6) #f(6) f(5) f(4) f(3) f(2) f(1) f(2) f(3) f(4)

Top-down vs. Bottom-up

  • 탑다운(메모이제이션): 하향식/ 보텀업: 상향식

    탑다운은 구현 과정에서 재귀 함수를 이용한다.

    즉, 큰 문제를 해결하기 위해서 작은 문제들을 재귀적으로 호출하여 작은 문제가 모두 해결되었을 때 실제로 큰 문제에 대한 답까지 얻을 수 있도록 코드를 작성한다.

  • 다이나믹 프로그래밍의 전형적인 형태는 보텀업 방식

    결과 저장용 리스트는 DP 테이블이라고 부른다.

  • 엄밀히 말하면 메모이제이션은 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미한다. 따라서 메모이제이션은 다이나믹 프로그래밍에 국한된 개념이 아니다.

  • 한 번 계산된 결과를 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수도 있다.

Top-down Source Code

# 한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
d = [0] * 100

# 피보나치 함수(Fibonacci Function)를 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
def fibo(x):
	# 종료 조건(1 혹은 2일때 1을 반환)
    if x==1 or x==2:
    	return 1
    # 이미 계산한 적 있는 문제라면 그대로 반환
    if d[x]!=0:
    	return d[x]
    # 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
    d[x] = fibo(x - 1) + fibo(x - 2)
    return d[x]
    
print(fibo(99))
#[실행 결과]
#218922995834555169026

Bottom-up Source Code

# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100

# 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1
d[2] = 1
n = 99

# 피보나치 함수(Fibonacci Function) 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for i in range(3, n + 1):
	d[i] = d[i - 1] + d[i - 2]
    
print(d[n])
#[실행 결과]
#218922995834555169026
  • 반복문을 이용해 점화식을 그대로 기입하여 차례대로 각각의 항에 대한 값을 구해나가는 것을 확인할 수 있다.
  • 즉, 작은 문제부터 먼저 해결해 놓은 다음에 먼저 해결해 놓았던 그 작은 문제들을 조합해서 앞으로의 큰 문제들을 차례대로 구해나가는 것을 확인할 수 있다.

How to do Dynamic Programming

  • 주어진 문제가 다이나믹 프로그래밍 유형임을 파악하는 것이 중요하다.

  • 가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지 검토할 수 있다.

    다른 알고리즘으로 풀이 방법이 떠오르지 않으면 다이나믹 프로그래밍을 고려해 보자.

  • 일단 재귀함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤에 (탑다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, (메모이제이션을 추가하여) 코드를 개선하는 방법을 사용할 수 있다.

  • 일반적인 코딩 테스트 수준에서는 기본 유형의 다이나믹 프로그래밍 문제가 출제되는 경우가 많다.

Comparison

Dynamic Programming vs 분할 정복

  • 다이나믹 프로그래밍과 분할 정복은 모두 최적 부분 구조를 가질때 사용할 수 있습니다. 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 상황
  • 다이나믹 프로그래밍과 분할 정복의 차이점: 분할 문제의 중복 - 다이나믹 프로그래밍 문제에서는 가 부분 문제들이 서로 영향을 미치며 부분 문제가 중복된다. - 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않는다.

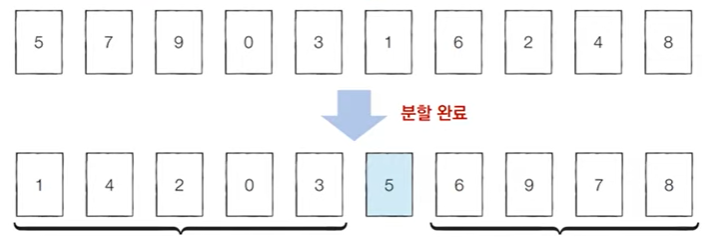
분할 정복의 대표적인 예시인 Quick Sort을 살펴보자.

  • 한 번 기준 원소(pivot)가 자리를 변경해서 자리를 잡으면 그 기준 원소의 위치는 바뀌지 않는다.
  • 분할 이후에 해당 피벗을 다시 처리하는 부분 문제는 호출하지 않는다.

img

Recursion vs. Dynamic Programming

Dynamic programming is mostly applied to recursive algorithms. This is not a coincidence, most optimization problems require recursion, and dynamic programming is used for optimization.

But not all problems that use recursion can use Dynamic Programming. Unless there is a presence of overlapping subproblems like in the Fibonacci sequence problem, a recursion can only reach the solution using a divide and conquer approach.

That is the reason why a recursive algorithm like Merge Sort cannot use Dynamic Programming because the subproblems are not overlapping in any way.

Greedy Algorithms vs. Dynamic Programming

Greedy Algorithms are similar to dynamic programming in the sense that they are both tools for optimization.

However, greedy algorithms look for locally optimum solutions, or in other words, a greedy choice, in the hopes of finding a global optimum. Hence greedy algorithms can make a guess that looks optimum at the time but becomes costly down the line and do not guarantee a global optimum.

Dynamic programming, on the other hand, finds the optimal solution to subproblems and then makes an informed choice to combine the results of those subproblems to find the most optimum solution.

Example 1: 개미 전사

  • 개미 전사는 부족한 식량을 충당하고자 메뚜기 마을의 식량창고를 몰래 공격하려고 합니다. 메뚜기 마을에는 여러 개의 식량 창고가 있는데 식량 창고는 일직선으로 이어져 있습니다.
  • 각 식량창고에는 정해진 수의 식량을 저장하고 있으며 개미 전사는 식량창고를 선택적으로 약탁하여 식량을 빼앗을 예정입니다. 이때 메뚜기 정찰병들은 일직선상에 존재하는 식량 창고 중에서 서로 인접한 식량창고가 공격받으면 바로 알아챌 수 있습니다.
  • 따라서 개미 전사가 정찰병에게 들키지 않고 식량창고를 약탈하기 위해서는 최소한 한 칸 이상 떨어진 식량창고를 약탈해야 한다.

img

img

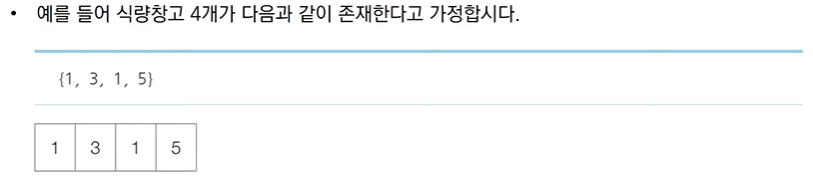
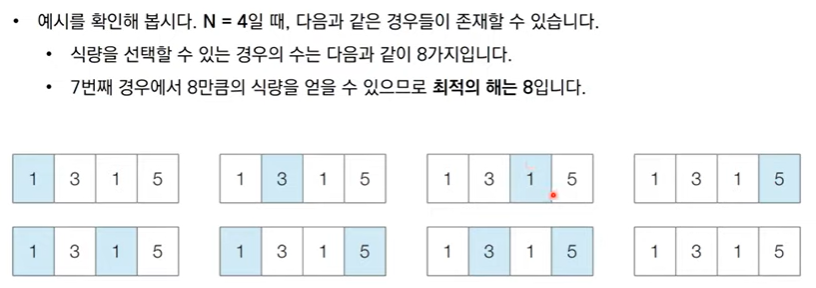
- 이때 개미 전사는 두 번째 식량창고와 네 번째 식량창고를 선택했을 때 최댓값인 총 8개의 식량을 빼앗을 수 있습니다. 개미 전사는 식량창고가 이렇게 일직선상일 때 최대한 많은 식량을 얻기를 원한다.

Q. 개미 전사를 위해 식량 창고 N개에 대한 정보가 주어졌을 때 얻을 수 잇는 식량의 최댓값을 구하는 프로그램을 작성하세요.

img

img

img

img

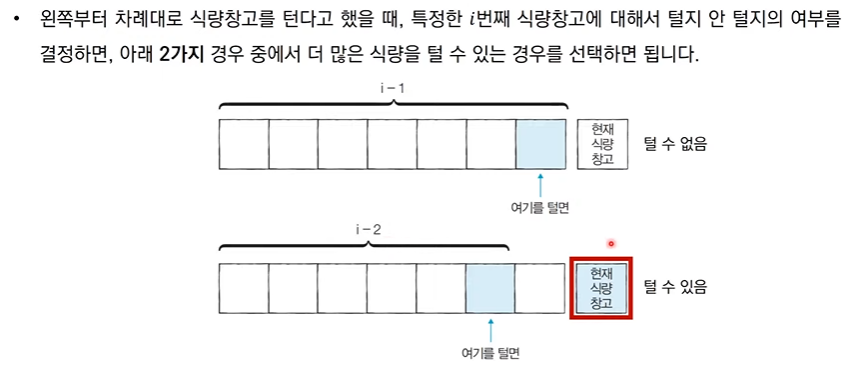
  • 큰 문제를 풀기 위해 작은 문제 두 개를 이용

img

Answer

# 정수 N을 입력 받기
n = int(input()) #4
# 모든 식량 정보 입력 받기
array = list(map(int, input().split())) # 1 3 1 5

# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0]*100

# 다이나믹 프로그래밍(Dynamic Programming) 진행 (Bottom-up)
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2,n):
	d[i] = max(d[i-1], d[i-2] + array[i])
    
# 계산된 결과 출력
print(d[n-1])

Example 2: 1로 만들기

  • 정수 X가 주어졌을 때, 정수 X에 사용할 수 있는 연산은 다음과 같이 4가지입니다.
1. X가 5로 나누어 떨어지면, 5로 나눕니다.
2. X가 3으로 나누어 떨어지면, 3으로 나눕니다.
3. X가 2로 나누어 떨어지면, 2로 나눕니다.
4. X에서 1을 뺍니다.
  • 정수 X가 주어졌을 때, 연산 4개를 적절히 사용해서 값을 1로 만들고자 합니다. 연산을 사용하는 횟수의 최소값을 출력하세요. 예를 들어 정수가 26이면 다음과 같이 계산해서 3번의 연산이 최소값입니다. 26 → 25 → 5 → 1

Greedy Algorithm로 풀면 비효율적. 26/2 보다는 26-1 =25로 시작하는 것이 연산의 최솟값.

img

img

img

  • a는 i번째 optimal solution.

Answer: 1로 만들기

# 정수 X를 입력 받기
x = int(input()) #26

# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0]*30001 #(1~30000 + 1)

# 다이나믹 프로그래밍(Dynamic Programming) 진행 (보텀업)
for i in range(2, x+1):
	# 현재의 수에서 1을 빼는 경우
    d[i] = d[i-1] + 1
    # 현재의 수가 2로 나누어 떨어지는 경우
    if i%2 == 0:
    	d[i] = min(d[i], d[i // 2] + 1)
    # 현재의 수가 3으로 나누어 떨어지는 경우
    if i%3 == 0:
    	d[i] = min(d[i], d[i // 3] + 1)
    # 현재의 수가 5로 나누어 떨어지는 경우
    if i%5 == 0:
    	d[i] = min(d[i], d[i // 5] + 1) #만약 더 작은 값이 있으면 업데이트할 수 있도록 모든 if에 min function을 넣어줌.
        
print(d[x]) #3

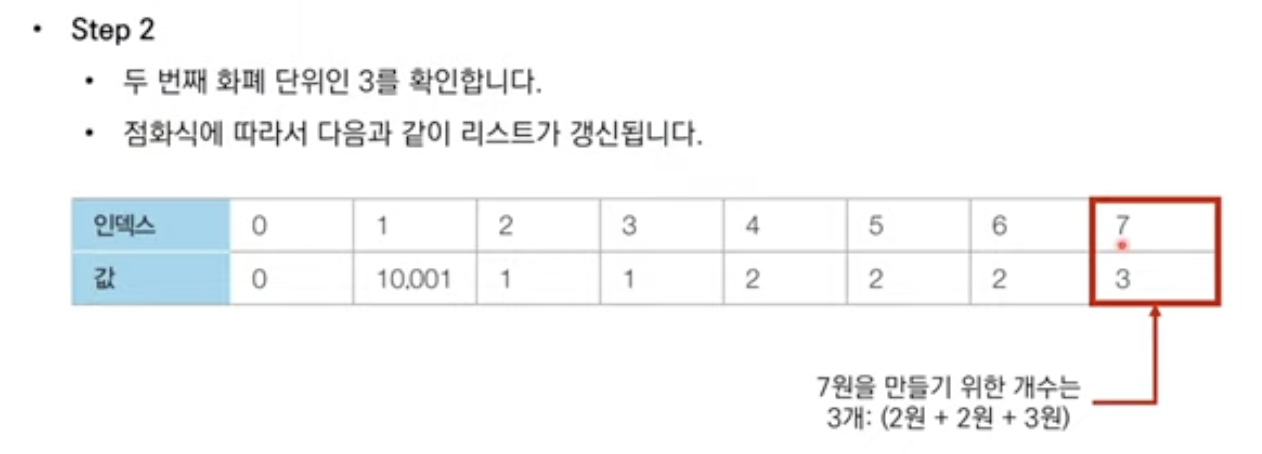
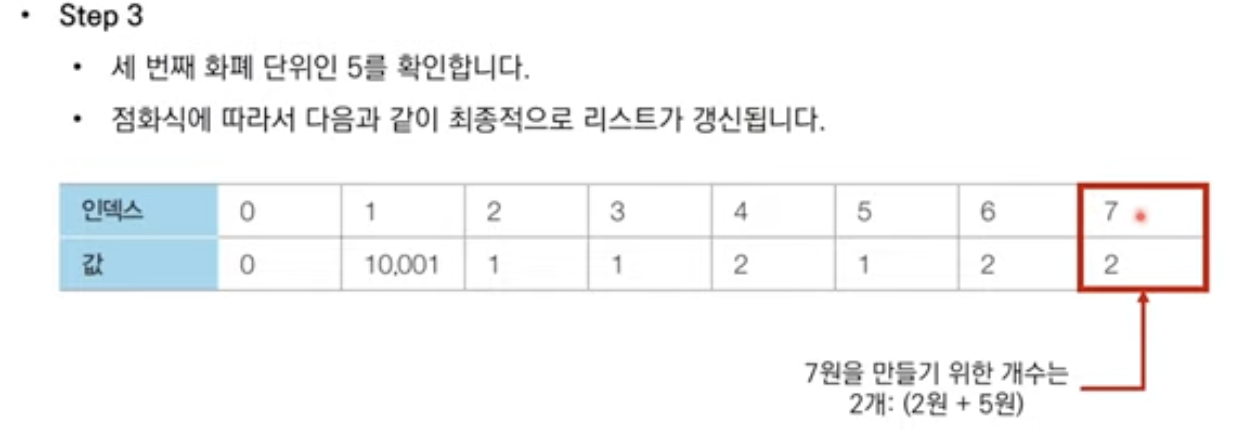
Example 3: 효율적인 화폐 구성

  • N가지 종류의 화폐가 있다. 이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려고 한다. 이때 각 종류의 화폐는 몇 개라도 사용할 수 있다.
  • 예를 들어 2원, 3원 단위의 화폐가 있을 때는 15원을 만들기 위해 3원을 5개 사용하는 것이 가장 최소한의 화폐 개수입니다.
  • M원을 만들기 위한 최소한의 화폐 개수를 출력하는 프로그램을 작성하세요.

img

img

image-20230502154150194

  • When k = 2, $a_i$ = 각 금액(인덱스) $i$를 만들 수 있는 최소한의 화폐 갯수.

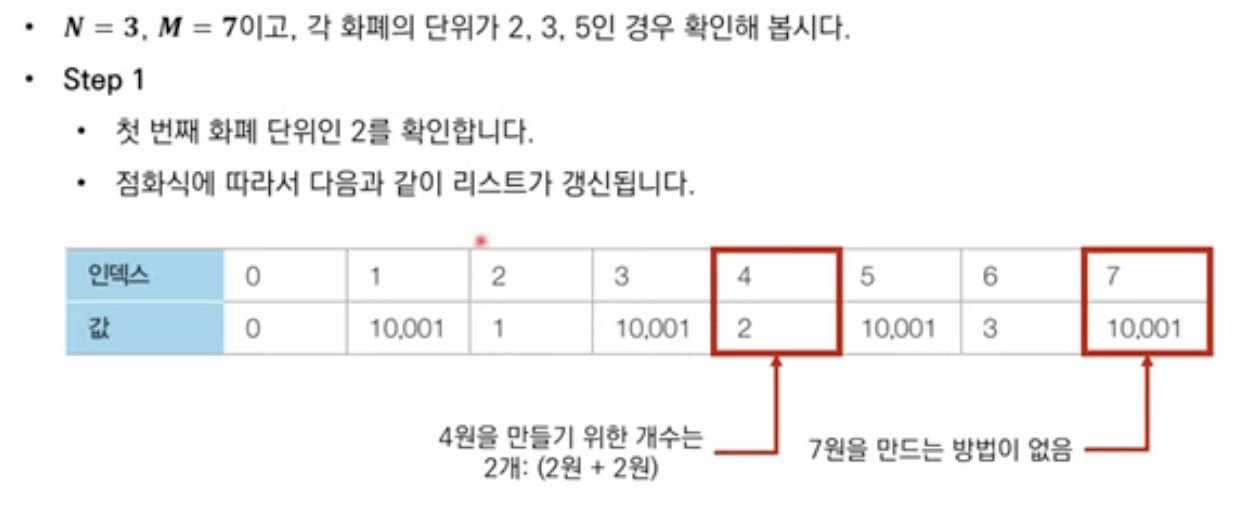
image-20230502154240257

image-20230502154735509

image-20230502154744746

Answer

# 정수 N, M을 입력받기
n, m = map(int, input().split())
# N개의 화폐 단위 정보를 입력받기
array = []
for i in range(n):
	array.append(int(input()))
    
# 한 번 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [10001]*(m + 1)

# 다이나믹 프로그래밍(Dynamic Programming) 진행(보텀업)
d[0] = 0
for i in range(n): #각각의 화폐단위
    for j in range(array[i], m + 1):
        if d[j-array[i]] != 10001:
            d[j] = min(d[j], d[j-array[i]]+1)

# 계산된 결과 출력
if d[m] == 10001:  # 최종적으로 M원을 만드는 방법이 없는 경우
	print(-1)
else:
	print(d[m])
  
#입력: 3 7
#2
#3
#5
#2

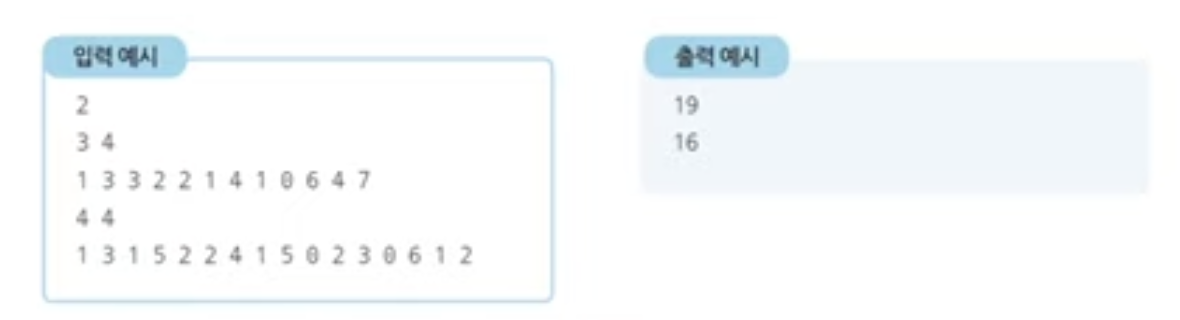
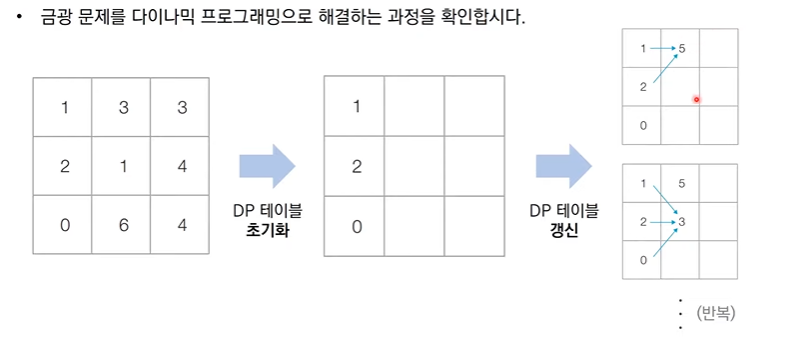
Example 4: 금광

  • nxm 크기의 금광이 있습니다. 금강은 1x1 크기의 칸으로 나누어져 있으며, 각 칸은 특정한 크기의 금이 들어 있습니다.
  • 채굴자는 첫 번째 열부터 출발하여 금을 캐기 시작합니다. 맨 처음에는 첫 번째 열의 어느 행에서든 출발할 수 있습니다.
  • 이후에 m-1번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 합니다.
  • 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 출력하는 프로그램을 작성하세요. img

img

image-20230502163624265

img

img

img

Answer

# 테스트 케이스(Test Case) 입력
for tc in range(int(input())):
	# 금광 정보 입력
    n,m = map(int, input().split())
    array = list(map(int, input().split()))
    
    # 다이나믹 프로그래밍을 위한 2차원 DP 테이블 초기화
    dp = []
    index = 0
    for i in range(n):
    	dp.append(array[index:index+m])
        index += m
        
    # 다이나믹 프로그래밍 진행 (Bottom-up)
    for j in range(1,m):
    	for i in range(n):
        	# 왼쪽 위에서 오는 경우
            if i==0:
            	left_up = 0
            else:
            	left_up = dp[i-1][j-1]
            # 왼쪽 아래에서 오는 경우
            if i==n-1:
            	left_down=0
            else:
            	left_down = dp[i+1][j-1]
            # 왼쪽에서 오는 경우
            left = dp[i][j-1]
            dp[i][j] = dp[i][j] + max(left_up, left_down, left)
    result = 0
    for i in range(n):
    	result = max(result, dp[i][m-1])
    print(result)

Example 5: 병사 배치하기

  • 부분 수열의 최대 길이!
  • N명의 병사가 무작위로 나열되어 있습니다. 각 병사는 특정한 값의 전투력을 보유하고 있습니다.
  • 병사를 배치할 때는 전투력이 높은 병사가 앞쪽에 오도록 내림차순으로 배치를 하고자 한다. 다시 말해 앞쪽에 있는 병사의 전투력이 항상 뒤쪽에 있는 병사보다 높아야 한다.
  • 또한 배치 과정에서는 특정한 위치에 있는 병사를 열외시키는 방법을 이용합니다. 그러면서도 남아 있는 병사의 수가 최대가 되도록 하고 싶습니다.

img

img

img

img

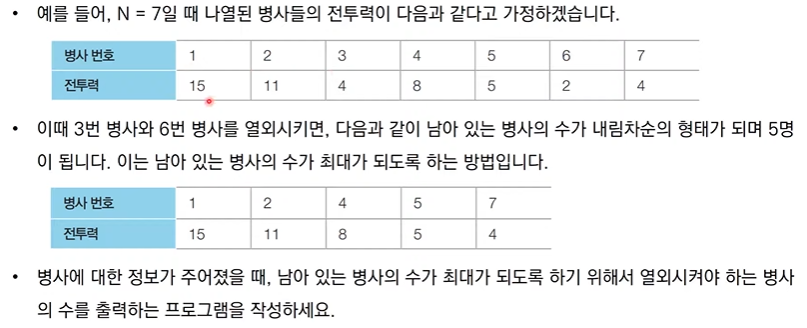
  • 가장 먼저 입력 받은 병사 정보의 순서를 뒤집습니다.
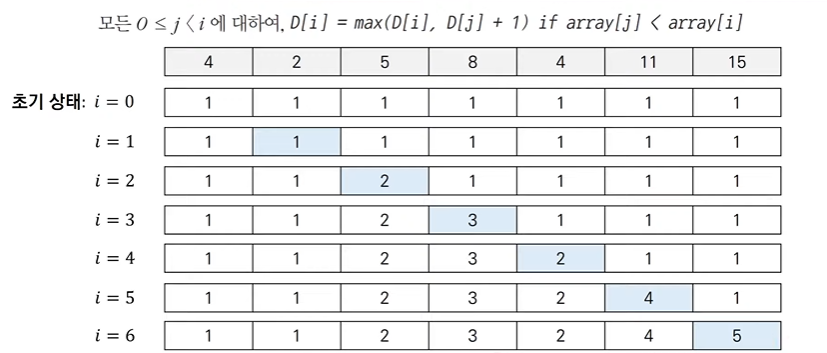
  • 가장 긴 증가하는 부분 수열 (LIS) 알고리즘을 수행하여 정답을 도출합니다.

Answer

n = int(input())
array = list(map(int, input().split()))

# 순서를 뒤집어 '최장 증가 부분 수열' 문제로 변환
array.reverse()

# 다이나믹 프로그래밍을 위한 1차원 DP 테이블 초기화
dp = [1]*n

# 가장 긴 증가하는 부분 수열(LTS) 알고리즘 수행
for i in range(1,n):
	for j in range(0,i):
    	if array[j]<array[i]:
        	dp[i] = max(dp[i], dp[j]+1)
            
# 열외해야 하는 병사의 최소 수를 출력
print(n-max(dp))

Leave a comment

You may also enjoy

Handling Missing Values

A perfect data set is usually a big win for any data scientist or machine learning engineer. Unfortunately, more often than not, datasets will have missing d...